1. 相关概念

1.1 实数、有理数、无理数、整数、自然数、虚数、复数

（1）实数【R：实数集】
实数（real number）是有理数和无理数的总称。

（2）有理数【Q：有理数集】
有理数（rational number）是可以表达为两个整数比（a/b, b≠0）的数。

（3）无理数
无理数（irrational number）是指有理数以外的实数。

（4）整数【Z：整数集】
整数（integer）是序列{...,-4,-3,-2,-1,0,1,2,3,4,...}中所有的数的统称，包括负整数、0和正整数。

（5）自然数【N：自然数集】
自然数（natural number）指非负整数(0,1,2,3,4,...)。

（6）虚数
虚数（imaginary number）是指可以写成实数与虚数单位i乘积的复数，即表示具有非零虚部的任何复数，可表达为z=a+bi（b≠0）。

（7）复数【C：复数集】
复数（complex number）是形如a+bi（a、b均为实数）的数，其中，a称为实部，b称为虚部，i为虚数单位。
复数通常用z表示，z=a+bi，当虚部b等于0时，通常称z为实数；当实部a等于0时，通常称z为纯虚数，可表达为z=bi（b≠0）。

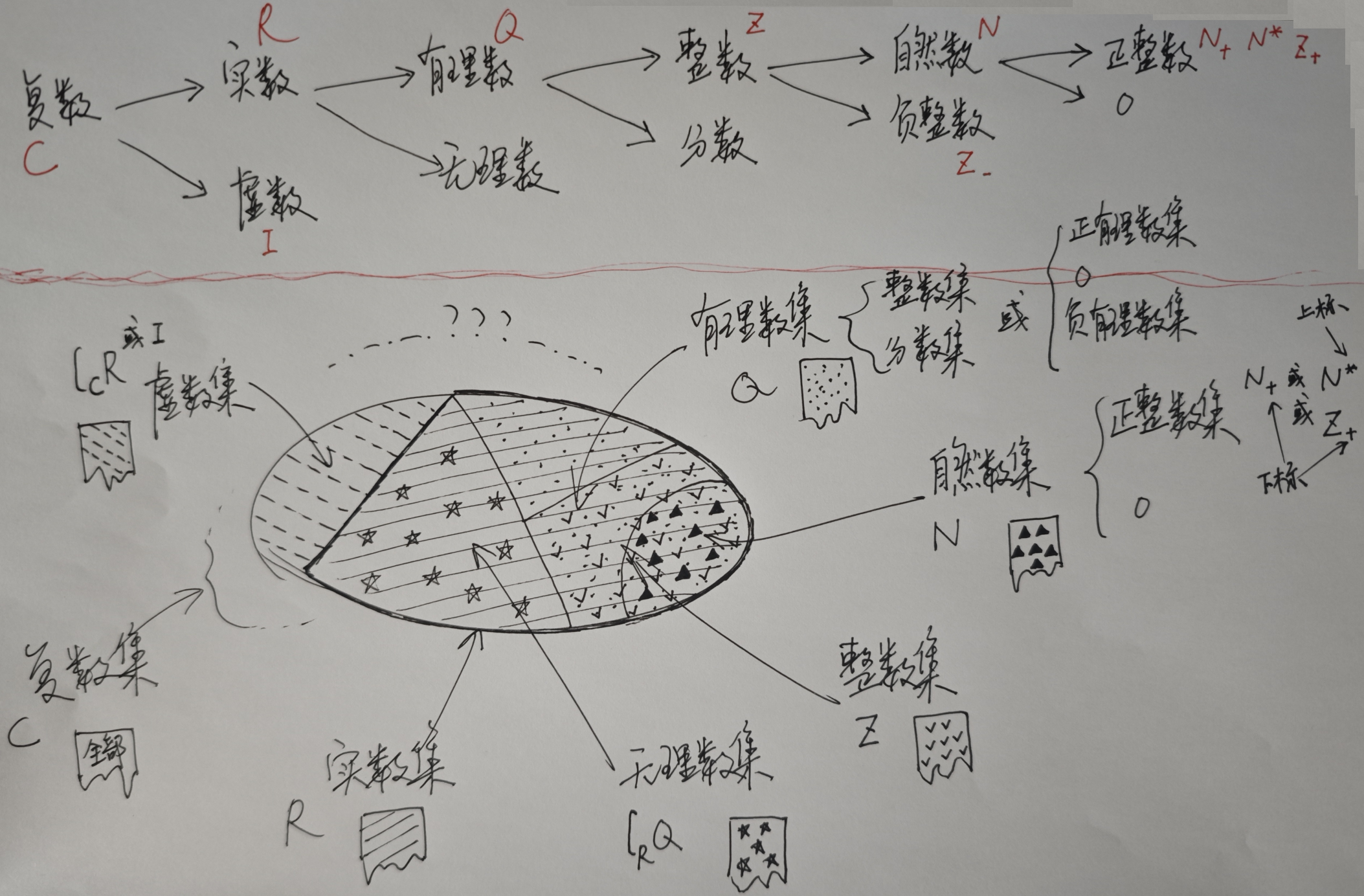
复数、实数、虚数、有理数、无理数、整数、分数、自然数、负整数、正整数、0……的关系如下图：

为什么任何实数都可以用无限小数来表示？

如果这个命题是真的，好处在于：统一，从某个维度体现有理数和无理数的共性，也就是可以统一地用无限小数来表示任何实数。

换言之，数轴（横轴）上任何一个数都可以用无限小数的形式来表示。

要证明“任何实数”都可以用“无限小数”来表示，需要各个击破，分别针对实数的每一个子类进行分析。
（1）正整数
例如：3=2.9999···

（2）0
规定：0=0.0000···

（3）负整数
例如：-3=-2.9999···

（4）分数
分数可以转化为有限小数和无限循环小数。
A. 有限小数
1/2 = 0.5 = 0.49999···

B. 无限循环小数
1/3 = 0.9999··· / 3 = 0.3333···

（5）无理数
无理数即无限不循环小数。

关键证明过程可参考下图中的部分内容：